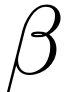path: root/man/numkondo.1

.Dd $Mdocdate: June 6 2022 $
.Dt numkondo 1.5
.Os
.Sh NAME
.Nm numkondo
.Nd A tool to iterate a flow equation numerically.
.Sh SYNOPSIS
.Nm
.Op Fl F
.Op Fl N Ar niter
.Op Fl I Ar initial_condition
.Op Fl P Ar precision
.Op Fl E Ar max_exponent
.Op Ar config_file
.Pp
.Nm
.Fl v
.Sh DESCRIPTION
.Nm
computes the numerical value of the iterates of a flow equation provided in its configuration file, starting from an initial condition provided in its configuration file.
.Nm
is part of a set of tools to compute and manipulate Fermionic hierarchical flows:
.Bl -bullet
.It
.Sy meankondo
: computes flow equations for hierarchical Fermionic models
.It
.Sy numkondo
: numerical evaluation of flow equations.
.It
.Sy meantools, meantools-convert
: perform various operations on flow equations (differentiation, products, sums, exponentials and logarithms of flow equations, evaluation and conversion to other formats).
.El
.Pp
.Sh COMMAND-LINE ARGUMENTS
.Bl -tag -width Ds
.It Fl N Ar niter
Number of iterations
.It Fl F
Only print the last step of the computation, with full precision. The output can be used as an initial condition for further iterations.
.It Fl I Ar initial_condition
Set the initial condition from the command-line (overrides the initial condition in the configuration file). The format is the same as the '#!initial_configuration' entry, see below.
.It Fl P Ar precision
Number of bits used for the significand of numerical values (see the NUMERICAL PRECISION section). If this option is specified, then numerical values are represented as MPFR floats instead of long doubles, which requires more computating time.
.It Fl E Ar max_exponent
Largest allowed value for the exponent of numerical values (see the NUMERICAL PRECISION section). If this option is specified, then numerical values are represented as MPFR floats instead of long doubles, which requires more computating time.
.It Fl v
Print version information and exit.
.El
.Pp
.Sh CONFIGURATION FILE
.Nm
reads a configuration file, that can either be passed as a command line argument or to stdin, which specifies the flow equation to iterate, the initial condition, and text labels for each running coupling constant.
.Pp
A configuration file is a list of entries, separated by a '&' character, each of which has a title (or header), which is preceded by '#!'. Note that '#!' must be at the beginning of a line in order to be read correctly.
.Pp
Whenever the '#' character is encountered, the rest of the line is treated as a comment and ignored (unless it is followed by '!').
.Pp
As a general rule, spaces and line breaks in the entries of the configuration file are ignored, so they may be used at the user's discretion. The few entries that require that no extra line breaks be inserted are explicitly mentioned below.
.Pp
.Nm
recognizes the following entries (unless explicitly mentioned, the entries below are mandatory) (entries may be provided in any order) (any extra entries in the configuration file are ignored):
.Bl -tag -width Ds
.It Sy #!flow_equation
The flow equation to be iterated.
.Pp
The flow equation has the same format as the output of
.Sy meankondo.
That is, a flow equation is a ',' separated list whose elements are of the form
.D1 [% index] = equation
where index is a non-negative integer or
.D1 [C index] = equation
where index is is a positive integer; and equation is formatted as explained below. [% index] stands for the running coupling constant corresponding to index, and [C index] is a special type of running coupling constant, which correspond to terms in the effective potential that do not depend on the fields. The difference between [% ...] and [C ...] is that the latter are evaluated first, and may be used in the equation of [% ...].
.Pp
Equations are '+' separated lists whose elements are monomials. Each monomial is a sequence of numbers, rccs and denominators:
.Bl -bullet
.It
Numbers are enclosed between '(' and ')'. If there are several numbers in a monomial, then they are multiplied.
.It
rccs are non-negative indices enclosed between '[%' and ']'.
.It
Denominators are of the form [/C index^power] and correspond to 1/C_index^power. Note that the denominators [C index] are computed before they are divided, and therefore, the equation corresponding to [C index] may not contain any [/C index^power].
.El
.Pp
If the numerical factor of a monomial is 1, then it can be dropped. However, even if the numerical factor is a single integer, its '(' and ')' delimiters cannot be omitted.
.Pp
In addition, in order to deal with derivatives of flow equations, extra running coupling constants can be introduced by adding any number of 'd' before '%' and 'C'. For instance, a flow equation may contain
.D1 [dd% index] = ...
or
.D1 [dC index] = ...
and an equation may contain an rcc of the form
.D1 [d% index]
.Pp
In practice, [C index] is represented as [%-index], and derivatives offset an index by 1000000, so [d% index] is equivalent to [%1000000+index], [dC index] to [%-1000000-index], [dd% index] to [%2000000+index], and so forth... Indices must therefore be smaller than 1000000 if 'd' is used.
.Pp
Example:
.D1 [C1] = [%1] + (1/2)[%1][%2] ,
.D1 [%1] = [%1][/C1^1] + [%1][%1][%2][/C1^2] ,
.D1 [%2] = [%2][/C1^1]
and with a derivative:
.D1 [C1] = [%1] + (1/2)[%1][%2] ,
.D1 [%1] = [%1][/C1^1] + [%1][%1][%2][/C1^2] ,
.D1 [%2] = [%2][/C1^1] ,
.D1 [dC1] = [d%1] + (1/2)[d%1][%2] + (1/2)[%1][d%2],
.D1 [d%1] = [d%1][/C1^1] + (-1)[%1][dC1][/C1^2] + (2)[%1][d%1][%2][/C1^2] + [%1][%1][d%2][/C1^2] + (-2) [%1][%1][%2][dC1][C1^3],
.D1 [d%2] = [d%2][/C1^1] + (-1)[%2][dC1][/C1^2]
.Pp
.It Sy #!initial_condition
The initial condition for the iteration.
.Pp
The initial_condition entry is a ',' separated list whose elements are of the form
.D1 index:value
where index is that of the corresponding rcc and value is a double precision float. The index may contain 'C' and 'd' characters as in the '#!flow_equation' entry.
.Pp
Example:
.D1 1:1.0 , 2:2.3e-6 , d1:2.0
.Pp
Note that if
.Nm
is called with the '-F' flag, the corresponding output is formatted in such a way that it can be used as an initial condition for other iterations.
.Pp
.It Sy #!labels
Labels for the running coupling constants, used as headers to display the flow of the iteration.
.Pp
The labels entry is a ',' separated list whose elements are of the form
.D1 index:"label"
where index is the non-negative index of the corresponding rcc, and label is a string.
.Pp
Example:
.D1 1:"one" , 2:"two"
.El
.Pp
.Sh OUTPUT
Unless the '-F' flag is provided,
.Nm
prints the result of the iteration at each step to stdout.
.Pp
If the '-F' flag is provided,
.Nm
prints the last step of the iteration to stdout in a format that can be re-used as an initial condition for subsequent iterations.
.Pp
.Sh NUMERICAL PRECISION
Numerical values are represented as floating point numbers, which consist in a significand (or mantissa) and an exponent. The number is given by
.D1 significand * 2^exponent
.Pp
If neither the '-P' nor the '-E' flags are specified, then numerical values are implemented using the 'long double' type, which allocates 64 bits to the significand and 15 to the exponent (this may change depending on the implementation of the C compiler used to compile
.Nm ) .
Numbers are therefore accurate to 19 decimal places, and the exponent must be in the interval [-16382 , 16383].
.Pp
If one of the '-P' or '-E' flags are specified, then numerical values are implemented using the GNU MPFR library. The number of bits allocated to the significand and exponent can be set by the '-P' and '-E' flags, within the limits set by the MPFR library. These values depend on the implementation of the library. On 64-bit systems, the maximal precision and maximal value of the exponent should be of the order of 2^63 and 2^62 respectively.
.Pp
Note that using MPFR floats increases the computing time required to run
.Nm
.Pp
.Sh RETURN CODE
.Nm
returns 0 on success and -1 on error.
.Pp
.Sh SEE ALSO
.Sx meankondo Ns (1) ,
.Sx meantools Ns (1) ,
.Sx meantools-convert Ns (1) ,
.Pp